Curs 3
https://www.pbinfo.ro/probleme/3860/consecutive1
RMQ = RANGE MINIMUM/MAXIMUM QUERY
RMQ[i][j] = min/max (a[i], a[i+1]......a[i+2^j-1]);
int rmq[NMAX][20];
int log2[NMAX];
rmq[2][0] = min(a[2],a[2])
rmq[2][1] = min(a[2],a[3])
rmq[2][2] = min(a[2],a[3],a[4],a[5]) = min(rmq[2][1],rmq[4][1])
......
rmq[2][17] = ......
......
rmq[3][0] = min(a[3],a[3])
log2[0] = 0;
log2[1] = 0;
for(int i = 2; i <= NMAX; ++i) {
log2[i] = log2[i/2] + 1;
}
5 10
a[5] a[6] a[7] a[8] a[9] a[10]
min(rmq[5][2],rmq[7][2])
x y
pw2 = log2[y-x+1];
min(rmq[x][pw2], rmq[y-(1<<pw2)+1][pw2]);
int query_min(int x, int y){
int pw2 = log2[y-x+1];
return min(rmq[x][pw2], rmq[y-(1<<pw2)+1][pw2]);
}
int main() {
for(int i = 1; i <= n; ++i)
rmq[i][0] = a[i];
for(int pw = 1; pw <= 18; ++pw)
for(int i =1 ; i <= n; ++i) {
rmq[pw][i]=min(rmq[pw-1][i], rmq[pw-1][i+(1<<pw-1)])
}
}
a[1][2]
RMQ = RANGE MINIMUM/MAXIMUM QUERY
RMQ[i][j] = min/max (a[i], a[i+1]......a[i+2^j-1]);
int rmq[NMAX][20];
int log2[NMAX];
rmq[2][0] = min(a[2],a[2])
rmq[2][1] = min(a[2],a[3])
rmq[2][2] = min(a[2],a[3],a[4],a[5]) = min(rmq[2][1],rmq[4][1])
......
rmq[2][17] = ......
......
rmq[3][0] = min(a[3],a[3])
log2[0] = 0;
log2[1] = 0;
for(int i = 2; i <= NMAX; ++i) {
log2[i] = log2[i/2] + 1;
}
5 10
a[5] a[6] a[7] a[8] a[9] a[10]
min(rmq[5][2],rmq[7][2])
x y
pw2 = log2[y-x+1];
min(rmq[x][pw2], rmq[y-(1<<pw2)+1][pw2]);
int query_min(int x, int y){
int pw2 = log2[y-x+1];
return min(rmq[x][pw2], rmq[y-(1<<pw2)+1][pw2]);
}
int main() {
for(int i = 1; i <= n; ++i)
rmq[i][0] = i;
for(int pw = 1; pw <= 18; ++pw)
for(int i =1 ; i <= n; ++i) {
if(nivel[rmq[pw-1][i]] < nivel[rmq[pw-1][i+(1<<pw-1)]]
....
rmq[pw][i]=min(rmq[pw-1][i], rmq[pw-1][i+(1<<pw-1)])
}
}
a[1][2]
//consecutive1
for(in....) {
cin >> x >>y;
min = min_qurery(x,y);
max = max_query(x,y);
if(max-min == y-x && D[y] <= x)
cout << 1;
else
cout << 0;
}
3 4 4 6
D[4] = 3
D[i] = j -> secventa de la j.....i este doar cu elemente distincte si este cea mai lunga
D[1] = 1
D[2] =
st = 1;
for(int dr = 1; dr<=n;++dr) {
f[a[dr]]++
if(f[a[dr]]==1)
D[dr] = st;
else
while(f[a[dr]]>1){
f[st]--;
st++;
}
}
st......dr -> valid => st+1.....dr - valid
sp[y] - sp[x-1]
https://www.infoarena.ro/problema/taxa
https://www.infoarena.ro/problema/volum
https://www.infoarena.ro/problema/mofocarburi
LCA
https://www.infoarena.ro/problema/lca
m=x+y+2z+2v , f=2x+z+u+2w si c=2y+2u+v+w .
x = 2xo + xrest
y = 2y0 + yrest
z = 2zo + zrest
w = 2w0 + wrest
m∙M + f∙F + c∙C = (x+y+2z+2v)*M + (2x+z+u+2w) * F + C* (2y+2u+v+w ) =(2x0 + x +2y0 + y +4zo + 2zo+ 4w0 + 2w) M
(2x0 + xrest +2y0 + yrest +4zo + 2zrest+ 4w0 + 2wrest) M
(2(x0 + yo + 2z0+zrest + 2w0 + wrest) + x + y) M + .... y + z C , z+w W
xrest = 0, yrest = 1 wrest = 0 zrest=0
Nr += F[(x-xrest)/2 + (y-yrest)/2 + w/2 + z/2])
map<str, int> mp
int nr_solutii(int m, int f, int c) {
if(m == 0 && f == 0 && c == 0)
return 1;
if(mp[{m,f,c}])
return mp[{m,f,c}]
if(mp[{f,m,c}])
return mp[{f,m,c}]
......
sau sortam m f c
M = par
for(int xrest = 0; xrest < 2; ++xrest)
for(int yrest= 0 ; yrest < 2; ++yrest)
for(int wrest = 0;
for(int zrest...
if((xrest+yrest)%2 == m%2. c%2 f%2){
rez += nr_solutii(((x-xrest)/2 + (y-yrest)/2 + w + c, ...., ...
}
m, f,c = (m-1)/2, f/, c + ...
}
PARCURGERE EULER
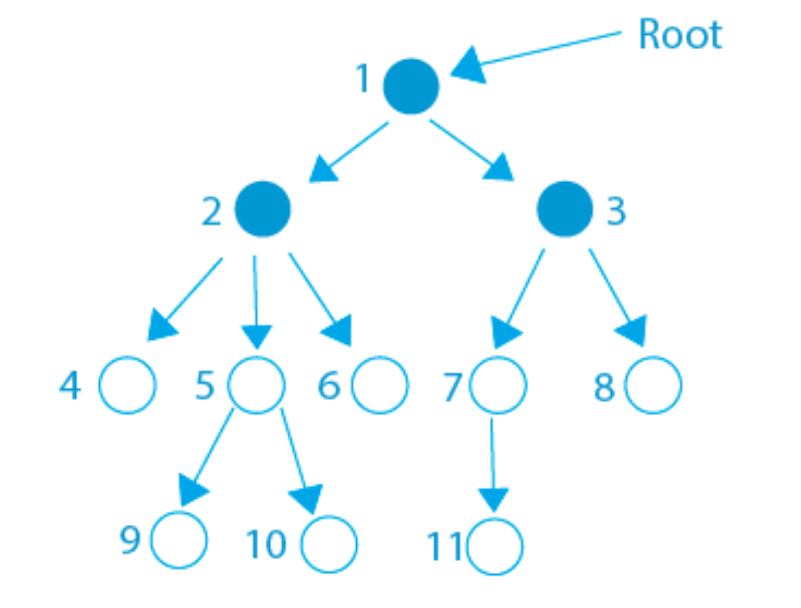
1 2 4 2 5 9 5 10 5 2 6 2 1 3 7 11 7 3 8 3 1
int euler[NMAX*2];
LCA
vector<int>G[NMAX];
void dfs(int x, int nv) {
viz[x] = 1;
euler[++cnt] = x;
euler_nivel[cnt] = nv;
first[x] = cnt;
for(auto vecin: G[x]) {
dfs(vecin,nv+1);
euler[++cnt] = x;
euler_nivel[cnt] = nv;
}
}
int LCA(int x, int y) {
int indice = rmq_euler_nivel(first[x], first[y])
return euler[indice];
return nodul cu nivelul minim din euler intre first[x],first[y].
}
#include <priority_queue>
pq
2 2 3 3 3
2 2 3 1 3
2 3 1 3 3
2 2 3 1 2
2 2 2 2 2
int main() {
h = INF
for(int i = 1; i<= n; ++i){
h[1][i] = a[1][i];
pq.push(a[i][1],i,1).
}
while(!pq.empty()) {
int i = ...
int j = ...
for(int k = 0; k < 3; ++k)
{ int ivecin = i + di[k];
int jvecin = j + dj[k];
if(h[ivecin][jvecin] > max(a[ivecin][jvecin],h[i][j]) {
h[ivecin][jvecin] = max(a[ivecin][jvecin],h[i][j]);
pq.push({h[ivecin][jvecin],ivecin,jvecin]});
}
}
}
s += h[i][j] - a[i][j];
}
DEFINITIE
DP[i] = cate propozitii pot sa fac cu primele i litere;
DP[i] = DP[i-1] + DP[i-2]+ ... DP[
c[1] c[2] ....c[i-4] c[i-3] c[i-2] | c[i-1] c[i]
.....zza[i-2] a[i-1] a[i]
int st=1;
int nr_voc_curent =
for(int i =1 ;i <= n; ++i) {
if(a[i] == vocala)
nr_voc_curent++;
if(nr_voc_curent > k) {
while(nr_voc_curent > k) {
++st;
if(vocala)
nr_voc_curent--;
}
}
dp[i] = sp[i-1] - sp[st-1];
sp[i] = sp[i-1] + dp[i];
}
k = 1;
i= 1;
i = 2;
k = 1